Common Lispでナイーブベイズをナイーブに実装

プログラミング Lisp 機械学習

精度を問わず簡単に使える分類器が欲しかったので、Common Lispでナイーブベイズ分類器cl-naive-bayesを作りました。

github.com

使い方は簡単です。まずは学習。学習結果を保持するlearned-storeを用意した後は、learn-a-document関数にこのstore，ドキュメント = 単語のリスト*1，カテゴリ（スパムメール判定であれば「スパム」or「非スパム」）の3つを渡すだけです。

(defparameter *store* (nbayes:make-learned-store))

; (カテゴリ 単語のリスト)
(defparameter *documents*
  (list '("A" ("a1" "a2" "a3" "a4" "ab"))
        '("A" ("a3" "a4" "a5" "a6"))
        '("B" ("b1" "b2" "b3" "b4" "ab"))
        '("C" ("c1" "c2" "c3"))))

(dolist (doc *documents*)
  (nbayes:learn-a-document *store* (cadr doc) (car doc)))

次に分類ですが、学習したstoreと単語のリスト（ドキュメント）をsort-category-by-prob関数に渡すだけです。以下のように事後確率の高い順にソートして出力してくれます。事後確率も同時に取得したい場合は、sort-category-with-post-probを使います。

(nbayes:sort-category-by-prob *store* '("a1" "ab" "c1" "new"))
=> ("A" "C" "B")

(nbayes:sort-category-with-post-prob *store* '("a1" "ab" "c1" "new"))
=> (("A" . 0.4211471) ("C" . 0.3527683) ("B" . 0.22608456))

解説の方針

ナイーブベイズ分類器自体についてはすでに良い解説があるので参考にしたリンクを張るにとどめ、作るには結局どうすんのさというところだけ書きます。ということでまずはリンクを。

データ構造

上で紹介したサイトは、アルゴリズムの解説は大変分かりやすいのですが、データ構造に関わる情報が分散していて分かりづらかったように記憶しています。ということで、アルゴリズムの解説は置いてデータ構造だけ説明しようと思います。データ構造が分かればできたようなものだという人もいるのできっと問題ないでしょう。

学習データとテストデータ

まず学習や分類（テスト）の一単位はドキュメントです。例えば、スパムメール分類であれば一つのメールが一つのドキュメントにあたります。ナイーブベイズ分類器がこのドキュメントをどう認識するかというと、単なる単語の羅列として認識します。これがナイーブたる所以で、文脈やら順序やら何もかも無視して、誰かがドキュメントを単語の羅列に分解したものを受け取ります。

また、学習データとテストデータの差は、前者が教師情報にあたるカテゴリ（文字列）を持っているという部分だけです。

学習用のlearn-a-document関数と、分類用のsort-category-by-prob関数のシグネチャを見るとおおむね了解できると思います。storeは次に述べる学習データを保持している構造体です。

; シグネチャのみ
; 例：word-lst: '("I" "am" "a" "pen"), category: "spam"
(defun learn-a-document      (store word-lst category))
(defun sort-category-by-prob (store word-lst))

学習結果の保持

導出は上記のリンクを参照して欲しい*2のですが、データ構造を決める上で必要な式だけ取り出します。

{ \displaystyle \begin{array}{l} P(cat|doc) = \frac{P(cat)P(doc|cat)}{P(doc)} \propto P(cat)P(doc|cat)\\ P(cat) = \frac{カテゴリの登場数}{ドキュメント数}\\ P(doc|cat) = \prod_{i} P(word_{i}|cat) = \prod_{i} \frac{カテゴリにおけるword_{i}の登場数}{カテゴリにおける全単語の登場数の和} \end{array} }

簡単に説明します。doc, catと並ぶとdogとcatに見えて仕方ないのですが、documentとcategoryです。第1式の事後確率P(cat|doc)が求めたいものです。値が大きいほど与えられたドキュメント（例．メール）がそのカテゴリ（例．スパム or スパムじゃない）に属する確率が高いということで、これを全カテゴリについて計算して比較します。計算方法が右辺になりますが、カテゴリ分けのためには大小関係だけ分かればよいので、カテゴリに依存しないP(doc)は除いて事前確率P(cat)と尤度P(doc|cat)だけを計算します。

第2式の事前確率P(cat)は見たままですが、分子・分母に「学習における」と接頭辞をつけるとより分かりやすいでしょうか。第3式の尤度P(doc|cat)を求めるためには、見ての通りとにかくカテゴリにおける各単語の登場数さえ覚えておけばよいことが分かります。なお、\prod_{i}の各要素は非常に小さい値になる場合が多いため、logをとって足し算として計算するのが普通のようです。cl-naive-bayesでも踏襲しています。

(defstruct learned-store
  (category-data-hash (make-hash-table :test #'equal))
  (num-document 0)
  (num-word-kind 0))

(defstruct category-data
  (count 0)
  (sum-word-count 0)
  (word-count (make-hash-table :test #'equal)))

ということでこのようになりました。全体として必要なデータ（learned-store）は学習したドキュメントの総数（num-document）とカテゴリごとのデータ（category-data-hash）になります。カテゴリごとに持っておくデータ（category-data）は学習した回数（count）と各単語の出現回数（word-count）です。

今記述しなかった二つのデータはキャッシュ（計算で求められるデータ）で、learned-storeのnum-word-kindは学習した単語の種類数であり、category-dataのsum-word-countはカテゴリ内での全単語の登場数の和です。後者はともかく前者は上記の式にも出ていませんが、ラプラス・スムージング（Laplace Smoothing）に利用します。この目的は、そのカテゴリで未知の単語が出てきたときにP(doc|cat)が0になることを避けることです。偉そうな名前がついていますが、単に初めての単語も1回出たものとして計算するという代物です。同様にn回出た単語はn+1回出たと考えるので、第3式の分子には1を足します。これを学習した全種類の単語で行うため、分母には単語の種類数を足します。ここで足す値がnum-word-kindです。

ここまで分かればアルゴリズムはほぼ自明だと思います。学習ではカテゴリと単語リストの組を受け取って、learned-storeの適切なスロットをカウントアップします。実際の分類では、上記の式に従ってP(cat|doc)の大小関係を計算するだけです。注意が必要なのは、計算過程ではlogをとるということと、ラプラス・スムージングぐらいです。

ソース全体は以下の通りです。ハッシュ内にデータがあるかないかで処理が変わる部分が多いため、anaphoraが大活躍しています。

cl-naive-bayes/cl-naive-bayes.lisp at master · eshamster/cl-naive-bayes · GitHub

cl-naive-bayesの実装上の工夫

特にないです…も悲しいので小さいものを二つ。

事後確率の求め方

一般的なナイーブベイズ実装にならい、事後確率の分母を無視して分子の（logの）大小比較のみでソートをしています。上記リンク先のPython実装では疑似的に事後確率を求める方法として、logで分子を求めた後にそれぞれexpをとった和で割って正規化するという方法が紹介されています。が、expに渡す値が-1000などという値になっていると、0しか返って来ないため計算できません。下記使用例のスパム判定のように超ナイーブな使い方をするとこういう値が普通に出てきます。ということで計算上の簡単な工夫ですが、(log a, log b, log c)の状態からいきなりexpをとるのではなく、全体からlog aを引いて(log 1, log b/a, log c/a)としてからexpをとっています。

incf-plus

学習用の関数learn-a-documentで使っています。適当に命名したので何も伝わらないと思いますが、引数なしincfの拡張版で、数値に対してはincfと同じく（破壊的に）1を足す一方で、nilの場合はエラーとせず1を代入する点が異なります。目的は下記のように何度もgethashを使うのを避けることです。

; これを…
(if (gethash word (category-data-word-count it))
    (incf (gethash word (category-data-word-count it)))
    (setf (gethash word (category-data-word-count it))))

; こうしたい
(incf-plus (gethash word (category-data-word-count it)))

実装はOn Lispの汎変数の章を参考に、define-modify-macroを使いました。

なお、元々はanaphoraのsif（aifと異なり代入可能なitが提供される）を使おうとしていましたが、上記例の通りすでにit（anaphoraのsletによる）を使っているため、意図通りに動きませんでした。

試しに使ってみる

バグチェックも兼ねてスパム判定を試してみようとroswellスクリプトを起こしました（データを用意する部分はshellスクリプトに逃げました）。

cl-naive-bayes/judge-spam.ros at master · eshamster/cl-naive-bayes · GitHub

英文のスパムメール判別コーパス（http://spamassassin.apache.org/publiccorpus/）の2002年版easy_hamとspamを使います。メール本文をいかにして単語のリストに変換するかが腕の見せどころ…のはずですが、tokenize-mail関数ではヘッダのタグも何もかも空白・改行区切りでリストにして分類器にぶち込むゴミ実装になっています（例えば、"From:"なんかは全部のメールに出そうです…）。さすがにこれだと60～70%ぐらいで頭打ちになりそうなので、簡単なヘッダ解析とか品詞分類ぐらいはしないと…と思って事前に調べていたのですが、意外と95%ぐらいまで正解していたので満足してしまった次第です*3。ナイーブベイズ恐るべし。

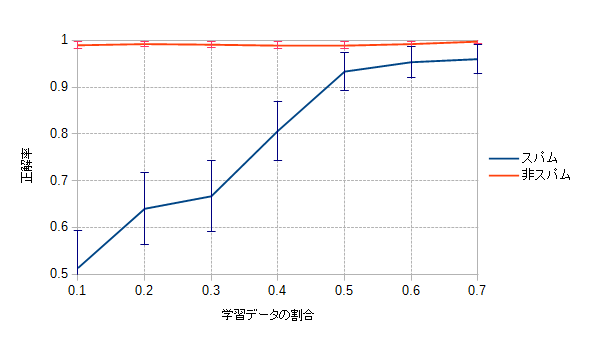
一応グラフを。テストデータを後ろから3割で固定し、学習データを前からX割で変化させた場合の正解率（5%信頼区間つき）です*4。全データ数は、非スパムが2546, スパムが497です。

f:id:eshamster:20151018145427p:plain

  • メモ
    • 日本語の形態素解析ではMeCabの名前を知っていたのですが、英語だと何があるのかと調べたところCommon Lispではg000001さんの公開されているtaggerが簡単に使えそうでした
    • コーパスの文字コードがそろっていなかったので、とりあえず"nkf --overwrite -w"しているのですが、変換元を指定しないためか不可思議な動きが見られました
      • 一回でUTF-8 or ASCIIにならないものがいくつかあったので見てみたのですが、変換を繰り返すと以下のような動きをするものが見つかりました。なんだこれ。
      • 今のところ、収束性に不安があるので1回目の変換でUTF-8 or ASCIIにならなかったものは一律削除しています。

できていないもの

  • ダンプやリストア
    • 実運用を考えると、DBに保管したりそこから復元したりという機能は必須でしょう。
    • 全ダンプだけでなくて、DB更新用にlearn-a-documentに更新差分を吐かせるようなオプションも必要でしょうね。実装面倒そうですが…。
  • 解析用の機能
    • カテゴリごとの事後確率の高い単語ランキングなんて面白そうです。
  • チューニング用の機能

*1:ここがイコールになるところがナイーブベイズの仮定です

*2:特に3つ目の式の最初の等号は、ナイーブベイズにおける単語の独立性の仮定があって初めて成り立つ式なので注意が必要です

*3:もちろん実用としては全く話になりませんが、まあテストとしては…

*4:judge-spam.rosの引数ですが、例えば"./judge-spam.ros 0.2 0.3"とすると、学習データを前から2割、テストデータを後ろから3割という意味になります