木構造の親子関係を考慮したソート
前置き
Common Lisp(サブセット)をJavaScriptコードに変換するParenscriptを色々拡張しているps-experimentで以前パッケージもどきを追加したことがありました。
単にuse-packageしているパッケージをたどっていって、その配下で定義したParenscript用関数をすべてJavaScriptに変換するという代物です。このときに、パッケージの出力順については「まあJavaScriptで出力順序が影響するケースも少ないだろうし、問題が起きた時に考えよう…」と思っていたのですが、とうとう問題が起きたので真面目に考えてみたというのが今回の発端です*1。
この出力順の問題は、一般化するとパッケージをノード、use-packageの関係をエッジ(useしている側が親、されている側が子)とした木構造として捉えられます。このノードを以下の条件を満たすように一列に並び替えます。
- 親ノードは子ノードよりも後ろに配置される
面倒なのは一つの子ノードが複数の親ノードを持つ可能性がある可能性や、循環参照が存在する可能性があるため、単なる深さ優先探索では不十分という点です。ひとまずは(1)親ノードは1つだけで循環参照も存在しないという条件から始めて、(2)循環参照はなしで親ノードを複数持てる場合、(3)循環参照をエラーにする場合、(4)循環参照を許可する場合*2と徐々に条件を厳しくして考えていきます。
たぶん世界中で100万人は考えたことのある問題です。
準備
コード込みで考えていきたいので、道具となる構造体や関数を定義しておきます。なおこの記事全般に言えることですが、コードは読み飛ばしてもだいたい意味は通る…はずです。
パッケージの依存関係処理に使いたいというのがそもそもの発端であったため、汎用に使えるようにgenericを定義しておきます。
(defgeneric get-node-name (node)) ; プリント用 (defgeneric node-equalp (node1 node2)) ; ノード間の等値比較 (defgeneric get-children (node)) ; 子ノードの取得
単純なnode構造体とメソッドを作成します。
(defstruct node name children) (defmethod get-node-name ((node node)) (node-name node)) (defmethod node-equalp ((node1 node) (node2 node)) (eq (node-name node1) (node-name node2))) (defmethod get-children ((node node)) (node-children node))
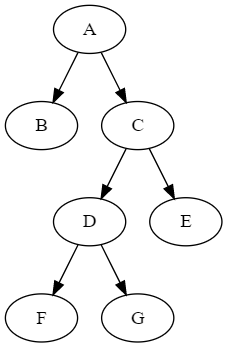
次に、実験用に木を簡単に構成するための補助関数を作成します。木の定義は((:parentA :childA1 :childA2) (:parentB :childB1 :childB2) ...)のように簡単に書けるようにします。例えば、上図の木の場合は次のように書き下します。
(defparameter *simple-tree* '((:a :b :c) (:c :d :e) (:d :f :g)))
これを、親子関係(node-children)を設定しながらnode構造体のリストにするのがmake-treeです。なおaifやitはanaphoraライブラリのものです。
(defun make-tree (parent-children-pair) (let ((node-pool (make-hash-table)) (result nil)) (flet ((ensure-node (name) (check-type name keyword) (aif (gethash name node-pool) it (setf (gethash name node-pool) (make-node :name name))))) (dolist (pair parent-children-pair) (let ((parent (ensure-node (car pair)))) (dolist (child-name (cdr pair)) (push (ensure-node child-name) (node-children parent))) (push parent result)))) (dolist (node result) (setf (node-children node) (nreverse (node-children node)))) result))
また、与えられたノードのリストの子供をたどって、重複なしに全てのノードを一列に並べる関数linearize-all-nodesを用意します*3。
(defun linearize-all-nodes (node-list) (let ((result nil)) (labels ((rec (node) (unless (some (lambda (target) (node-equalp target node)) result) (push node result) (dolist (child (get-children node)) (rec child))))) (dolist (node node-list) (rec node))) result))
本題
段階1:親ノードを一つしか持てず循環参照も存在しない木の場合
まずは1番単純な、親ノードを一つしか持てず循環参照も存在しない、下図のような木を考えます。

こうした木の場合は一番上のノードを取り出して、そこから深さ優先探索を行うだけで問題ありません。この制約下では、深さ優先探索で子ノードが親ノードよりも先に訪問されることはないためです。
(defun sort-tree-node-simply (node-list) (let ((top-node (find-if (lambda (target) ;; If the target is not child of any node, it is a top node. (notany (lambda (parent) (some (lambda (child) (node-equalp target child)) (get-children parent))) node-list)) node-list))) (assert top-node) ;; linealize-all-nodes が深さ優先探索であることを仮定しています。汚いですがまあ前座なので… (linearize-all-nodes (list top-node))))
ソートした結果を表示するための関数(以降使いまわします)を作って結果を見てみると、正しくソートされていることが分かります。
(defun print-result (tree sort-fn) (format t "~A~%" (mapcar #'get-node-name (funcall sort-fn (make-tree tree))))) (print-result *simple-tree* #'sort-tree-node-simply) ;; -> (E G F D C B A)
段階2:複数の親を許すが循環参照は存在しない木の場合
次に、循環参照はないものの、ノードに複数の親を持つことを許した木を考えます。下図の例では、ノードFはAとDの2つの親を持ちます。
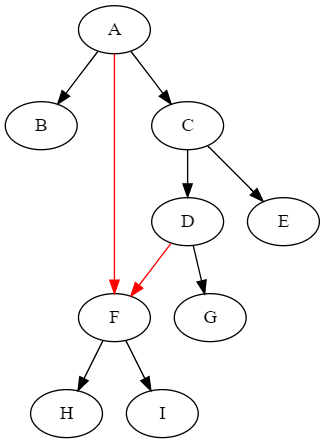
(defparameter *duplicated-tree* (make-tree '((:a :b :f :c) (:c :d :e) (:d :f :g) (:f :h :i))))
これを段階1の深さ優先ソートで出力してみると…
(print-result *duplicated-tree* #'sort-tree-node-simply) (E G D C I H F B A)
子であるFが出てくる前にDが出てきてしまっています。その親子関係まで見ると"DC"と"IHF"を入れ替えないと正しい結果にならないことが分かります。複数の親を許したために、A→Fというより早く探索されるパスができてしまったためにうまくいかなくなりました。
そこで、全ノードのリストからソート済みリストへ移すときに、既に子ノードがすべて後者の移されているかをチェックする機構を入れる必要があります。あとは、全ノードリストからチェックを通るものを一つずつピックアップしてソート済みリストに持っていくだけです。第1段階で仮定していたような、全ノードの取得部分linearize-all-nodesが深さ優先探索であるという仮定もいらなくなります。
;; 子ノードが全てソート済みリストに入っているかをチェックする ;; (ここではまだ関係ありませんが、自己参照は無視しています) (defun all-children-are-processed (node processed-node-list) (every (lambda (child) (or (node-equalp node child) ; Ignore self dependency (find child processed-node-list :test #'node-equalp))) (get-children node))) (defun sort-tree-node-with-duplication (node-list) (labels ((rec (rest-nodes result) (aif (find-if (lambda (node) (all-children-are-processed node result)) rest-nodes) (rec (remove it rest-nodes :test #'node-equalp) (cons it result)) result))) (reverse (rec (linearize-all-nodes node-list) nil))))
結果を見ると、今度はノードDとCの前にI, H, Fが全て出てきており、正しい順番にソートされることが分かります。
(print-result *duplicated-tree* #'sort-tree-node-with-duplication) ;; -> (B E G I H F D C A)
段階3:循環参照を検知してエラーにする
次は循環参照の存在する木を考えます。下図は「F→G→D→F→G→D→…」の循環参照が存在する木です。
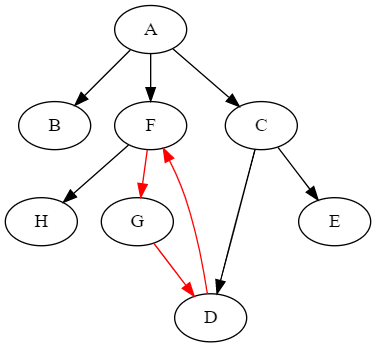
(defparameter *circular-tree1* '((:a :b :f :c) (:f :h :g) (:g :d) (:d :f) (:c :d :e)))
循環参照部分は「親ノードは子ノードよりも後ろに配置される」という条件を決して満たせないため、検知してエラーにする必要があります。なお、試しに前節のsort-tree-node-with-duplicationで並び替えてみると…循環参照を形成するF, G, Dの他、それらに依存するA, Cも巻き込まれて出力されません。
(print-result *circular-tree1* #'sort-tree-node-with-duplication) ;; -> (B E H)
さて、まずは循環参照を検出する関数extract-circular-nodesを作成します。内部関数recが本体になりますが、深さ優先探索で木を探索しながら、トップから現在ノードまでの経路をtraverse-listに格納しています。新たに辿ろうとした子ノードがtraverse-listに既に含まれていた場合、循環参照が存在することが分かります。また、このときtraverse-listの先頭から同リスト内の子ノードまでが循環経路になります(コード上ではtraverse-listをreverseしてmemberで子ノード以降を取り出すという操作をしています)。この辺りのアイディアは、後述のASDFでの循環参照検知方法を参考にしています(というよりそのままです)。なお、自己参照も循環参照の一種ではありますが、害はないので素通しにしています。
(defun extract-circular-nodes (node-list) (labels ((rec (current-node traverse-list) (setf traverse-list (cons current-node traverse-list)) (dolist (child (get-children current-node)) (unless (node-equalp current-node child) ; Ignore self dependency (when (find child traverse-list :test #'node-equalp) (let ((result (member child (reverse traverse-list) :test #'node-equalp))) (return-from rec result))) (let ((next-result (rec child traverse-list))) (when next-result (return-from rec next-result))))) nil)) ;; ※通過済みのノードであってもチェックすることになるので ;; さすがにちょっとバカっぽいループです… (dolist (node node-list) (awhen (rec node nil) (return-from extract-circular-nodes it)))))
後はこれを利用して循環参照をエラーにするチェック関数を用意して、sort-tree-node-with-duplicationの手前に設置すれば、循環参照をエラーにするsort-tree-node-checking-circularの完成です。
(defun check-circular-dependency (node-list) (awhen (extract-circular-nodes node-list) (error "There is (a) circular dependency: ~A" (mapcar #'get-node-name it)))) (defun sort-tree-node-checking-circular (node-list) (check-circular-dependency (linearize-all-nodes node-list)) (sort-tree-node-with-duplication node-list))
次のように、循環参照を検知してエラーにしつつ、そうでなければsort-tree-node-with-duplicationと同等のソート性能を持つことが分かります。
(print-result *duplicated-tree1* #'sort-tree-node-checking-circular) ;; -> (B E G I H F D C A) (print-result *circular-tree* #'sort-tree-node-checking-circular) ;; -> (次のようなエラーを出力)There is (a) circular dependency: (F G D)
余談:ASDFにおける循環参照検知
ここで余談ですが、今回パクった参考にしたASDFのコードについてです。
ASDFでは.asdファイルにdefsystemでシステムを定義しますが、ここで各モジュールを構成するファイル間の依存関係を定義します。asdf:load-system時にはこれを見て、循環参照があればエラーにしています。実際にエラーを検知してエラーを出力しているのはasdf.lispの下記call-while-visiting-actionです。なお、これは1ノード分の処理であり、木の探索自体はより上位の関数で実行します。
若干用語を補足します。
action: 今回で言うノードに当たるようですaction-list: 今回でいうtraverse-listで、現在の通過経路が入ったリストですaction-set:actionをキーとし、ブール値を値とするハッシュです。ここでは通過経路にt、それ以外にnilを入れているようです*4
循環参照の検知をしているのは(gethash action action-set)で、通過経路に現在のactionがあるかを判定しています。検知した場合は、循環参照エラーにします。このとき、action-listをreverseしてmemberで現在のaction以降を取り出すことで、循環経路を取り出しています。…というように、ハッシュを使っている以外はそのまま参考にしました。
;; ※ASDF 3.1.5のコードより (defmethod call-while-visiting-action ((plan plan-traversal) operation component fun) (with-accessors ((action-set plan-visiting-action-set) (action-list plan-visiting-action-list)) plan (let ((action (cons operation component))) (when (gethash action action-set) (error 'circular-dependency :actions (member action (reverse action-list) :test 'equal))) (setf (gethash action action-set) t) (push action action-list) (unwind-protect (funcall fun) (pop action-list) (setf (gethash action action-set) nil)))))
段階4:循環参照ノードをグループ化して解決する
※警告:この段階4は実用性が微妙なくせに説明がとても長いです…
循環参照がある時点で基本的におかしいので、即エラーの段階3まででも良い気もします。ただ、ASDFにおけるファイル間の循環参照とは違い、パッケージ間の循環参照については検知される契機がないため、どこかでやらかしているライブラリがあると詰む可能性が考えられます。そのため、将来的な逃げ道のために循環参照をある程度いなして解決する方法を考えておきます。

ここで、改めて循環参照の存在する木を眺めてみると、循環参照をグループ化して一つの塊だと思えばうまくいきそうです。つまり、FGDを1つのグループと見て、FGDはHに依存し、AとCはそれぞれFGDに依存しているといった具合です。そして、同じグループに属するノードの出力順は任意で良いことにします。さて、図を見ながら考えると、グループやグループ間の等値性、グループ間の依存は下記のように定義できそうです*5。なお、ノードとグループを別個に扱うのは面倒そうなので、ノード1つの「塊」もグループとして扱うことにします。
- 定義:グループ
- 1つ以上のノードから構成され、かつ、
- 2つ以上のノードが存在する場合、グループ内の全ノードを含む循環参照が存在する
- 要は循環参照をグループ化しますということです
(defstruct node-group nodes ; グループを構成するノードのリスト children ; 子グループのキャッシュ ; (後述の「グループ間の依存」の定義に従い、依存するグループを集めたもの) )
- 定義:グループの等値比較
- グループAとグループBが等値であるとは、構成するノードが同じであることを言う
- 1つのノードは必ずある1つのグループだけに属しているという制約を設けるため、実際にはノードが1つでも一致すれば等値です
- グループAとグループBが等値であるとは、構成するノードが同じであることを言う
(defmethod node-equalp ((node1 node-group) (node2 node-group)) (let ((first-node (first (node-group-nodes node1)))) ;; An empty group is not allowed. (assert first-node) (find first-node (node-group-nodes node2) :test #'node-equalp)))
- 定義:グループ間の依存
- グループAがグループBに依存しているとき、グループAに含まれるノードの子ノードのうち、少なくとも1つがBに含まれる
(defun group-depend-p (target base) (some (lambda (base-node) (some (lambda (target-node) (find target-node (get-children base-node) :test #'node-equalp)) (node-group-nodes target))) (node-group-nodes base)))
(きちんと証明する能がないですが…)こうした定義から下記の性質を持つ点が重要です。
性質
- グループはノードとしての性質(等値比較ができる、子供を定義できる)を満たす
- 循環参照する複数のグループに属するノードを集めることで、一つのグループを構成できる
- 同一グループ内の任意の2ノードは循環参照している
- つまりグループ内のノード間では上下関係を決定できません
- 循環参照の関係にないグループA, Bがあり、かつAがBに依存しているとき、Bの全てのノードはAのどのノードから見ても(一方向の)子孫ノードである
- 平たく言えば、ノード間の親子(先祖/子孫)関係はグループ化しても保存されるということです
これらの性質を利用すると、下記のような手順で「循環参照を塊とみなしたソート」を実現できます
手順
- ノードのリストから、各ノードを要素とするグループのリストを作成する
- グループのリストから(自己参照でない)循環参照を探す。なければ手順5へ飛ぶ
- 性質1により、ノード用の循環参照検知関数をそのまま利用できる]
- 手順2で見つけた循環参照グループからノードを取り出して一つのグループにまとめ(性質2による)、元のグループは破棄する
- この操作によりリストの要素が減るので、無限ループにならない
- 手順2へ戻る
- グループをノードとみなし(性質1による)、段階2:複数の親を許すがループは存在しない木の場合に従ってソートする
- 手順5でソートされた順にグループを取り出し、含まれるノードを取り出してリストとする。このリストのノードは正しくソートされている(性質4による)
- 同一グループ内のノードの順序は任意でよい(性質3による)
手順1~4の実装は次のようになります。
;; ※循環参照グループをまとめる際に親子関係が変わるため、 ;; 再計算用の関数を用意 (defun calc-group-children (group group-list) (remove-if (lambda (target) (not (group-depend-p target group))) group-list)) (defun recalc-groups-children (group-list) (dolist (group group-list) (setf (node-group-children group) (calc-group-children group group-list))) group-list) ;; 手順3: 循環参照するグループ内のノードを一つのグループにまとめる (defun gather-ciruclar-node-group (circular-list group-list) (let ((new-group (make-node-group :nodes (apply #'append (mapcar (lambda (group) (node-group-nodes group)) circular-list))))) (recalc-groups-children (cons new-group (remove-if (lambda (group) (find group circular-list :test #'node-equalp)) group-list))))) ;; 手順1~4の一連の操作: グループ間の全ての循環参照をまとめあげる (defun make-group-resolving-circular (all-node-list) (labels ((rec (group-list) (aif (extract-circular-nodes group-list) (rec (gather-ciruclar-node-group it group-list)) group-list))) (rec (recalc-groups-children (mapcar (lambda (node) (make-node-group :nodes (list node))) all-node-list)))))
後は手順5に従い、make-group-resolving-circularの結果をsort-tree-node-with-duplicationに渡すことでグループ間のソートは完了です*6。
(defun sort-tree-node-with-circular (top-node-list) (sort-tree-node-with-duplication (make-group-resolving-circular (extract-all-nodes-by-dfs top-node-list))))
なお、見た目としてはグループをまとめたままの方が分かり易いため、以降では手順6(グループ内ノードのフラット化)を省略して出力します。
上記の循環参照する木をソートした結果を見ると、グループDFGがまとまり、またそれらに依存するA, Cは後から出てくるなど正しくソートできています。
((B) (E) (H) (D F G) (C) (A))
また、複数の循環参照を含む木でうまく動くかを確認するため、2つほど例を見てみます。
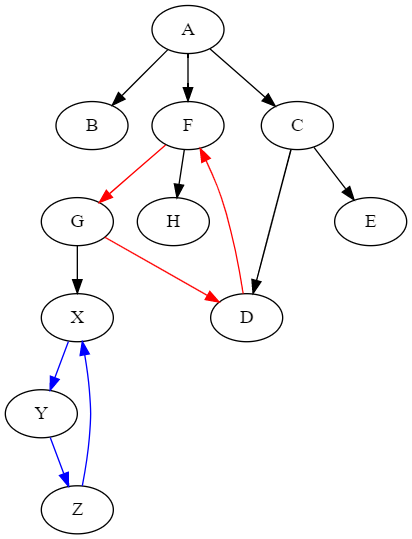
(defparameter *circular-tree2* '((:a :b :f :c) (:f :h :g) (:g :d :x) (:d :f) (:c :d :e) (:x :y) (:y :z) (:z :x))) ;; → ((B) (E) (H) (X Y Z) (D F G) (C) (A))
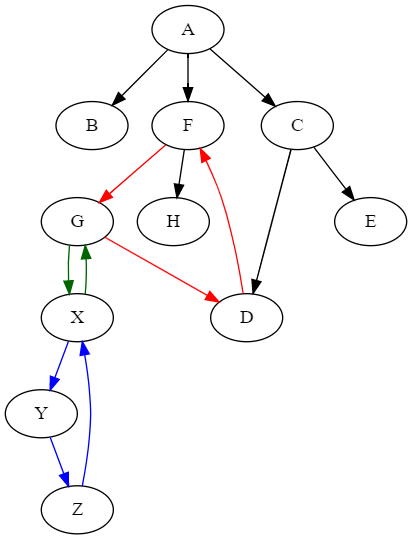
(defparameter *circular-tree3* '((:a :b :f :c) (:f :h :g) (:g :d :x) (:d :f) (:c :d :e) (:x :y :g) (:y :z) (:z :x))) ;; → ((B) (E) (H) (X Y Z D F G) (C) (A))
なお、グループ自体もノードとしての性質を満たすため、グループを要素としたグループを(再帰的に)作成できるはずですが、特に実用的な価値はないと思われます。
コード全体
最後に、全コードを貼り付けます。
Sort nodes in tree according to their dependencies …
Roswellスクリプトとして実行でき、下記を出力します。
$ ./sort-tree-node-with-circular.ros -------------------- --- Sort simply --- -------------------- *SIMPLE-TREE*: ((A B C) (C D E) (D F G)) -> (E G F D C B A) *DUPLICATED-TREE*: ((A B F C) (C D E) (D F G) (F H I)) -> (E G D C I H F B A) -------------------- --- Sort considering duplicated parent --- -------------------- *SIMPLE-TREE*: ((A B C) (C D E) (D F G)) -> (B E G F D C A) *DUPLICATED-TREE*: ((A B F C) (C D E) (D F G) (F H I)) -> (B E G I H F D C A) *CIRCULAR-TREE1*: ((A B F C) (F H G) (G D) (D F) (C D E)) -> (B E H) -------------------- --- Sort checking circular --- -------------------- *DUPLICATED-TREE*: ((A B F C) (C D E) (D F G) (F H I)) -> (B E G I H F D C A) *CIRCULAR-TREE1*: ((A B F C) (F H G) (G D) (D F) (C D E)) ERROR: There is (a) circular dependency: (F G D) -------------------- --- Sort considering circular --- -------------------- *SIMPLE-TREE*: ((A B C) (C D E) (D F G)) -> ((F) (G) (D) (E) (C) (B) (A)) *DUPLICATED-TREE*: ((A B F C) (C D E) (D F G) (F H I)) -> ((H) (I) (F) (G) (D) (E) (C) (B) (A)) *CIRCULAR-TREE1*: ((A B F C) (F H G) (G D) (D F) (C D E)) -> ((E) (B) (H) (F G D) (C) (A)) *CIRCULAR-TREE2*: ((A B F C) (F H G) (G D X) (D F) (C D E) (X Y) (Y Z) (Z X)) -> ((E) (B) (H) (X Y Z) (F G D) (C) (A)) *CIRCULAR-TREE3*: ((A B F C) (F H G) (G D X) (D F) (C D E) (X Y D) (Y Z) (Z X)) -> ((E) (B) (H) (D F G X Y Z) (C) (A)) -------------------- --- (Test self dependncy) --- -------------------- *TREE-TO-TEST-SELF-DEPENDENCY*: ((A A B F C) (C C D E) (D F G) (F H I)) -> (B E G I H F D C A) *TREE-TO-TEST-SELF-DEPENDENCY*: ((A A B F C) (C C D E) (D F G) (F H I)) -> (B E G I H F D C A) *TREE-TO-TEST-SELF-DEPENDENCY*: ((A A B F C) (C C D E) (D F G) (F H I)) -> ((H) (I) (F) (G) (D) (E) (C) (B) (A))
以上
*1:具体的には、ps-experimentで実装しているdefstructのサブセットで問題が起こりました。includeした場合に継承関係をつけるコードを出力するのですが、このコードが親となる構造体の定義よりも先に出てきてしまうと、うまく継承関係を定義できないようでした
*2:「親ノードは子ノードよりも後ろに配置される」をそのままでは満たせないため、少し条件を緩和して考えます
*3:パッケージの親子関係をたどるケースを考えると、最初に全てのパッケージが並んでいるのではなく、起点となるいくつかのパッケージを与えられるのが普通だと思います。ソートの中で徐々に展開しても良さそうですが、最初にすべて並べてしまった方が簡単そうなのでこうした関数を用意しています
*4:循環参照のチェックが終わると、action-setのキーの集合が全actionのリストとなる辺り賢いです。そこまで見ていないのですが、この後ロードを行う際にここでロード済みか否かを管理するのではないかと予想しています。ちなみに、ハッシュの値としてnilを入れておく(≒キーが存在しないことと同等に扱う)手法の実用的な価値をイメージできていなかったのですが、初めて分かった気がします
*5:というように「グループ」を素直に扱えば解決できるという所に行きつくまでに、実はすごい迷走してました…
*6:万全を期するのであれば、循環参照が確かに解消されたことを確認するために、check-circular-dependencyを入れた方が良いです